皮亞諾曲線（Peano curve）是一條能夠填滿正方形的曲線。

皮亞諾曲線（英語：Peano curve）是一條能夠填滿正方形的曲線。

在傳統概念中，曲線的數維是1維，正方形是2維。

1890年，義大利數學家朱塞佩·皮亞諾（義大利語：Giuseppe Peano）發明能填滿一個正方形的曲線，叫做皮亞諾曲線，其構造方法如下：取一個正方形並且把它分出九個相等的小正方形，然後從左下角的正方形開始至右上角的正方形結束，依次把小正方形的中心用線段連接起來；下一步把每個小正方形分成九個相等的正方形，然後上述方式把其中中心連接起來……將這種操作手續無限進行下去，最終得到的極限情況的曲線就被稱作皮亞諾曲線。

   

皮亞諾對區間 {\displaystyle [0,1]} [0,1]上的點和正方形上的點的對應作了詳細的數學描述。實際上，正方形的這些點對於 {\displaystyle t\in [0,1]} t\in [0,1]，可規定兩個連續函數 {\displaystyle x=f(t)} x=f(t)和 {\displaystyle y=g(t)} y=g(t)，使得 {\displaystyle x} x和 {\displaystyle y} y取屬於單位正方形的每一個值。後來，希爾伯特作出了這條曲線。

一般來說，一維的東西是不可能填滿2維的方格的。但是皮亞諾曲線恰恰給出了反例。

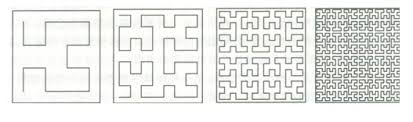
這說明我們對維數的認識是有缺陷的，有必要重新考察維數的定義。

這就是分形幾何考慮的問題。在分形幾何中，維數可以是分數叫做分維。

此外皮亞諾曲線是連續的但處處不可導的曲線。

因此如果我們想要研究傳統意義上的曲線，就必須加上可導的條件，以便排除像皮亞諾曲線這樣的特例。